Algorithme combinatoire

Principes de l’algorithme

L’algorithme de chaînage utilisé par cubr-link a été conçu et développé par cubr. Son objectif est de déterminer à quel individu de la base cible correspond chaque individu de la base source.

Cet algorithme “combinatoire” est une extension d’une approche déterministe traditionnelle où l’on cherche quels indidivus des bases de données source et cible partagent les mêmes caractéristiques. Dans la mesure où l’on ne peut utiliser un identifiant commun unique entre les deux bases, on utilise en effet un ensemble de N variables dites de chaînage qui sont communes entre les deux bases de données à chaîner (date de naissance, code postal, etc…) et dont chaque combinaison peut faire office d’identifiant unique pour chaque individu; si l’on repère une telle combinaison pour un individu unique de la base source et un individu unique de la base cible, on peut considérer que ces deux individus représentent la même personne et donc que l’on a chaîné ces deux individus entre les deux bases.

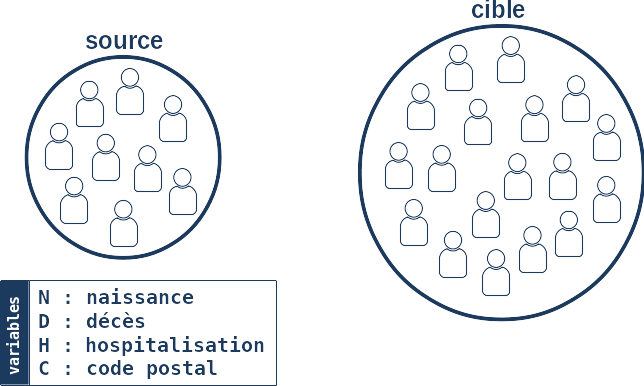
Dans cette approche, on doit donc commencer par choisir ces N variables de chaînage. Dans l’exemple qui suit, nous choisirons 4 variables comprenant à la fois des données socio-démographiques (date de naissance et de décès, code postal) et des données de parcours de soins (date d’hospitalisation).

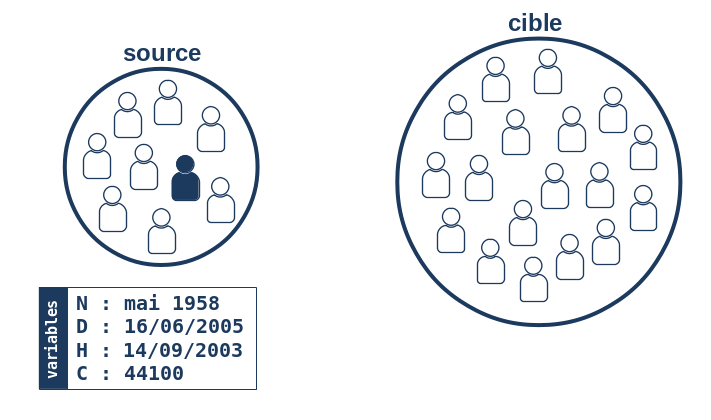
Pour chaque individu de la base source, l’algorithme repère quelles sont les valeurs prises par les 4 variables de chaînage. Dans l’exemple qui suit, nous choisirons un individu de la base source né en mai 1958 et décédé le 16 juin 2005, ayant eu une hospitalisation le 14 septembre 2003 et ayant été domicilié au code postal 44100.

L’algorithme va ensuite chercher dans la base cible quels sont les individus qui possèdent ces 4 caractéristiques, ou bien uniquement 3 caractéristiques parmi les 4, ou bien 2, etc… Plus généralement, il va chercher quels sont les individus de la cible qui possèdent K caractéristiques parmi les 4 possibles, K variant de 4 à 1.

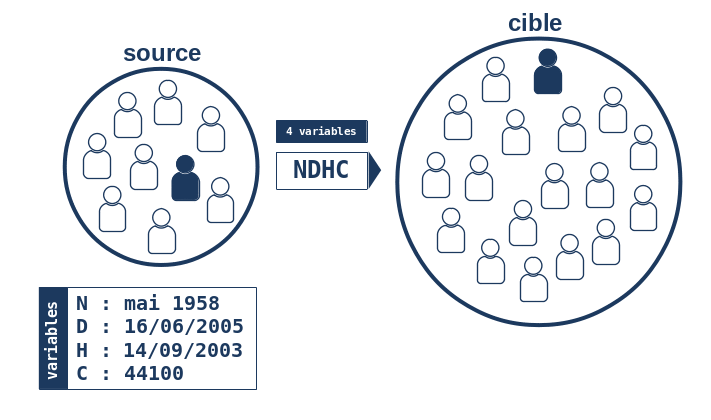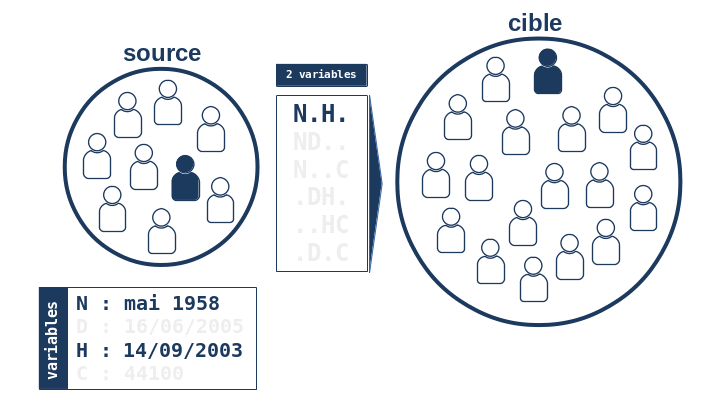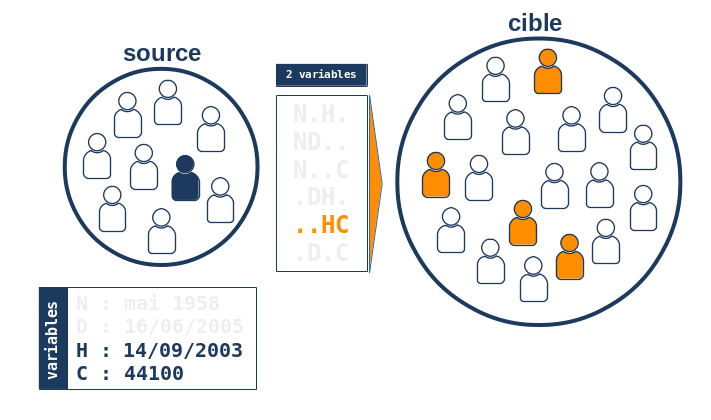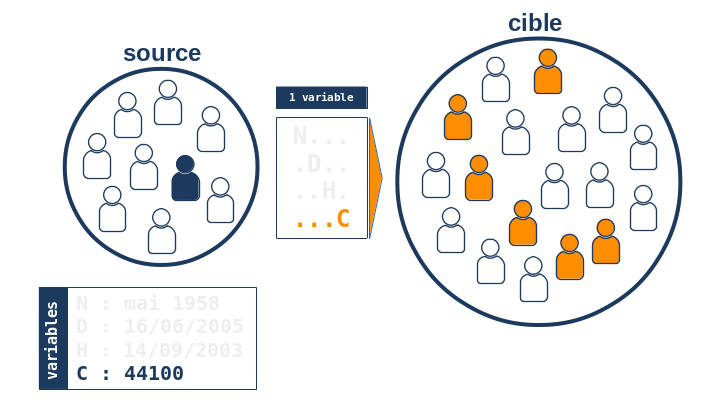
On constate que l’algorithme essaie toutes les combinaisons possibles de 4 variables (exceptée la combinaison de 0 variables sans intérêt ici), c’est à dire 2⁴-1 = 15 combinaisons et retient l’ensemble U des combinaisons produisant toujours le même indidividu unique dans la base cible. En particulier, l’ensemble U contient une combinaison “maximale” de 4 variables et donc l’algorithme considère qu’il a trouvé la bonne correspondance à l’individu de la base source, i.e. il est parvenu à trouver une paire chaînée entre un individu de la source et un individu de la cible.

Le graphique suivant montre pour l’exemple les combinaisons de l’ensemble U (en bleu) par rapport aux autres combinaisons ne produisant pas le candidat unique.

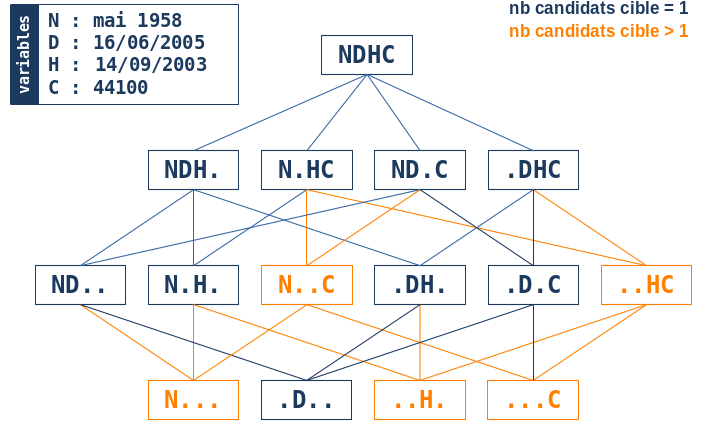
L’intérêt majeur de cette approche combinatoire provient du fait de l’exploration exhaustive de toutes les combinaisons possibles de variables de chaînage: s’il existe un individu unique dans la base cible qui maximise l’utilisation de l’information disponible, l’algorithme le trouvera nécessairement. En d’autres termes, on peut s’attendre à une très bonne sensibilité de l’algorithme. Un autre point essentiel vient de la possibilité de définir la notion de robustesse d’une paire chaînée comme étant le nombre de variables que l’on peut omettre tout en conservant la même paire chaînée. Dans l’exemple, on a vu que toutes les combinaisons de 4 et 3 variables produisaient le même candidat unique dans la base cible; il fallait enlever au moins deux variables pour perdre son unicité. Dans cet exemple, la robustesse de la paire est donc de 1.

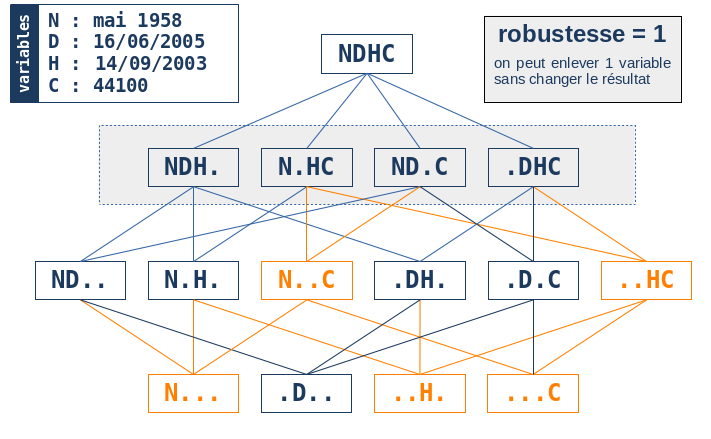
La notion de robustesse est une métrique qualitative importante pour juger de la pertinence d’une paire trouvée par l’algorithme. On comprend en effet que plus la robustesse est grande, plus on peut avoir confiance dans le résultat. A contrario, une robustesse de 0 (la plus petite valeur possible) signifie que l’algorithme a bien trouvé une paire chaînée mais qu’il ne peut plus enlever n’importe quelle variable sans perdre l’unicité de la paire. Dans un tel cas, l’utilisateur peut avoir envie avec son expertise métier de regarder plus précisément les caractéristiques des paires trouvées afin de voir s’il décide de conserver tout ou partie de ces paires de robustesse 0. De façon générale, une robustesse de 1 et plus indique que l’on peut avoir une bonne confiance dans les paires trouvées.

Cartographie du chaînage

Dans un projet de chaînage sur données réelles, il arrive très souvent que l’on ait des informations manquantes ou bien des erreurs dans les données. Du point de vue de l’algorithme de chaînage combinatoire, la conséquence est qu’un individu de la base source peut effectivement posséder 4 caractéristiques (i.e. variables NDHC dans l’exemple) mais que le vrai positif dans la base cible ne possède pas l’information relative à l’hospitalisation (variable H). Dans un tel cas, la force de l’algorithme combinatoire est que la combinaison de 3 variables “ND.C” (le point dénote ici l’absence de la variable H) sera tout de même vérifiée, avec potentiellement la possibilité de trouver le vrai positif dans la base cible.

Outre la bonne sensibilité de l’algorithme combinatoire qui se trouve encore ici justifiée, on constate qu’une paire chaînée est à la fois caractérisée par les deux individus (x,y) qui ont été chaînés par l’algorithme, mais aussi par l’information qui a été effectivement utilisée: l’individu x de la source est caractérisé par son profil “NDHC” et l’individu y de la cible est caractérisé par son profil “ND.C”; autrement dit, la variable “H” est manquante dans le profil de l’individu y de la cible. Donc, une façon de décrire une telle paire est d’écrire, en ajoutant l’information de robustesse :

source=NDHC, cible=ND.C, robustesse=1

Il devient dès lors extrèmement intéressant de stratifier les paires trouvées par profil source, profil cible et robustesse. Le tableau suivant décrit une telle stratification sur un chaînage utilisant 5 variables NDHUC (on a ajouté la variable U pour un passage aux urgences). On notera que le profil cible est indiqué dans ce tableau comme complément du profil cible dans le profil source, c’est-à-dire que l’on note uniquement les variables “manquées”. Par exemple, “…..” indique que toutes les variables disponibles dans le profil source ont bien été retrouvées dans le profil cible, alors que “.D…” indique que la variable D n’a pas été retrouvée. A titre d’exemple, l’algorithme a trouvé ici 11 paires de robustesse 1 avec les variables NDHUC disponibles dans le profil source et la variable D manquante dans le profil cible.

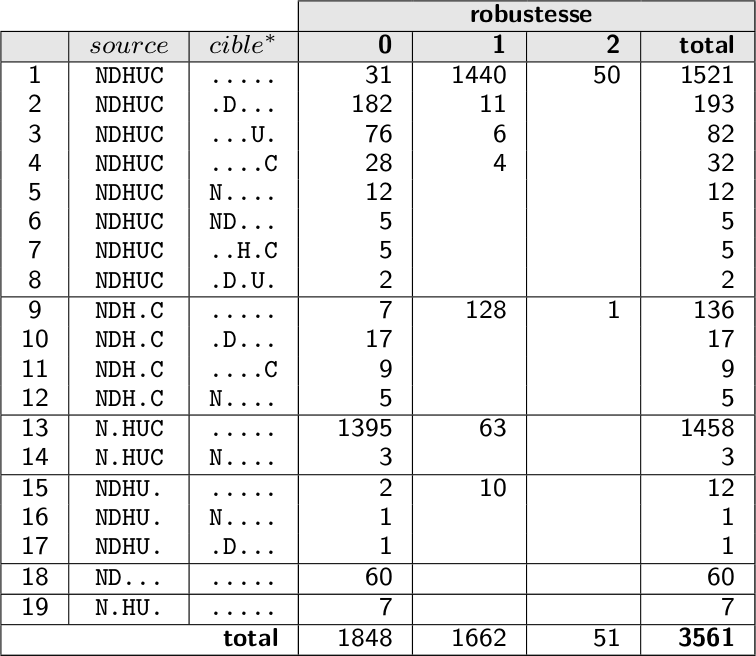
Un tel tableau représente une véritable cartographie du chaînage réalisé et offre un outil puissant pour permettre à l’utilisateur d’avoir un regard critique sur les résultats en fonction de sa connaissance des données. Ce dernier pourrait par exemple:

valider systématiquement les colonnes de robustesse >=1
valider les groupes de robustesse 0 et sans information manquée dans le profil cible (“…..”)
étudier au cas par cas les autres groupes. Par exemple, sa connaissance des données pourrait lui indiquer que la variable D n’est pas toujours bien renseignée; dans un tel cas, les profils cible “.D…” et de robustesse 0 pourraient être validés
etc…

Le point important de cette cartographie est aussi de redonner la main à l’expert qui décide au final ce qui doit être retenu ou non des résultats et donc de pouvoir utiliser a posteriori une connaissance métier des données que l’algorithme ne peut pas avoir. Cette capacité d’interpréter les résultats de l’algorithme et de décider en conséquence est une caractéristique essentielle rendue possible par l’algorithme de chaînage combinatoire et permet d’aller bien au dela du simple taux d’appariement qui est parfois le seul indicateur remonté par d’autres méthodes.

Performances de l’algorithme

L’approche combinatoire présentée ici peut a priori paraître gourmande en temps de calcul. En effet, le nombre d’opérations effectuées par l’algorithme est théoriquement de l’ordre de S*C*2^N, où S est le nombre d’individus dans la base source, C est le nombre d’individus dans la base cible et N est le nombre de variables de chaînage. Dans l’exemple présenté ci-dessus, on a S*C*2^N = 9*16*2⁴ = 2304. On comprend déjà que pour de grandes bases de données et pour un nombre de variables de chaînage important, ce nombre peut rapidement devenir gigantesque. A titre d’exemple, pour S=30.000, C=3.000.000 et N=8 (ce qui correspond à un projet de chaînage réaliste), ce nombre est supérieur à 20.000 milliards d’opérations à effectuer. En faisant des hypothèses raisonnables sur le temps d’exécution d’une opération sur un ordinateur de bureau, un tel chaînage durerait au minimum 5 jours.

L’implémentation développée par cubr permet de casser la complexité algorithmique propre à l’approche et d’obtenir à la fois des temps de calcul très raisonnables sur des machines de puissance conventionnelle ainsi que la possibilité d’attaquer de vastes volumétries de données. L’exemple proposé ci-dessus qui durerait plus de 5 jours est exécuté par cubr-link en 3 secondes sur une machine 4 coeurs et 16 GB de mémoire. Ce temps de calcul serait encore réduit sur une machine comportant davantage de coeurs de calcul.

Ces performances montrent d’une part que l’approche combinatoire est réalisable en pratique avec les avantages que l’on a vus précédemment, et d’autre part ouvrent des perspectives intéressantes sur la façon d’aborder la problématique du chaînage. Avec des temps de calcul très réduits, il devient possible pour l’utilisateur d’atteindre une forme d’interactivité avec la possibilité de faire varier certains paramètres, de lancer l’algorithme, d’évaluer les résultats et éventuellement adapter les paramètres puis relancer l’algorithme, etc… C’est précisément cette forme d’interactivité qui est introduite par l’interface graphique de cubr-link et qui permet de transformer la pratique du chaînage; la vidéo montrant cubr-link à l’oeuvre illustre parfaitement ce point.